ΕΝΗΜΕΡΩΣΗ-ΨΥΧΑΓΩΓΙΑ-ΕΚΠΑΙΔΕΥΣΗ

Πιάσε ένα φύλλο Α4... οι διαστάσεις του είναι 21×29,7 cm. Ειλικρινά, γιατί οι δημιουργοί του αποφάσισαν να μας βασανίζουν με αυτό το "περίεργο" 29,7 αντί για ένα καθαρό, στρογγυλό 30; Φαίνεται σαν να χάθηκε ένα μικρό κομμάτι στο τυπογραφείο. Η αλήθεια είναι ότι αυτό το «κομμάτι» που λείπει είναι στην πραγματικότητα το κλειδί για μία από τις πιο έξυπνες μαθηματικές εφευρέσεις στην καθημερινότητά μας. Το χαρτί Α4 δεν υπακούει στους "στρογγυλούς" κανόνες, αλλά στους αυστηρούς νόμους ενός άρρητου αριθμού: της ρίζας του 2. Αυτός ο αριθμός (≈1.414) είναι ο κρυφός αρχιτέκτονας που εξασφαλίζει ότι το χαρτί σου είναι... μαθηματικά τέλειο.

Πριν ξεκλειδώσουμε το μυστικό του χαρτιού, πρέπει να γνωρίσουμε τον πρωταγωνιστή μας. Η ρίζα του 2 είναι ένας άρρητος αριθμός. Τι σημαίνει αυτό; Φανταστείτε έναν αριθμό που, όσο και να προσπαθήσεις, δεν μπορείς να τον γράψεις σαν ένα τέλειο κλάσμα, και τα δεκαδικά του ψηφία συνεχίζουν στο άπειρο (≈1.41421356...) χωρίς ποτέ να επαναλαμβάνονται. Είναι σαν μια ιστορία που δεν τελειώνει ποτέ! Ο ρόλος του στο χαρτί είναι απλός, αλλά επαναστατικός: είναι ο μοναδικός λόγος διαστάσεων (Μήκος προς Πλάτος) που επιτρέπει σε ένα ορθογώνιο να διατηρεί ακριβώς την ίδια αναλογία όταν το κόψεις ακριβώς στη μέση.

Το σύστημα ISO 216 είναι, ουσιαστικά, ένα οικογενειακό δέντρο σελίδων χαρτιού όπου όλα τα μεγέθη είναι τέλεια αντίγραφα των προγόνων τους. Όλα ξεκινούν από τον «πατριάρχη» της οικογένειας, το Α0. Αυτό το τεράστιο φύλλο χαρτιού έχει ένα ακόμη εντυπωσιακό μυστικό: η έκτασή του είναι ακριβώς 1 τετραγωνικό μέτρο (1m²), με διαστάσεις 1189mm×841mm.

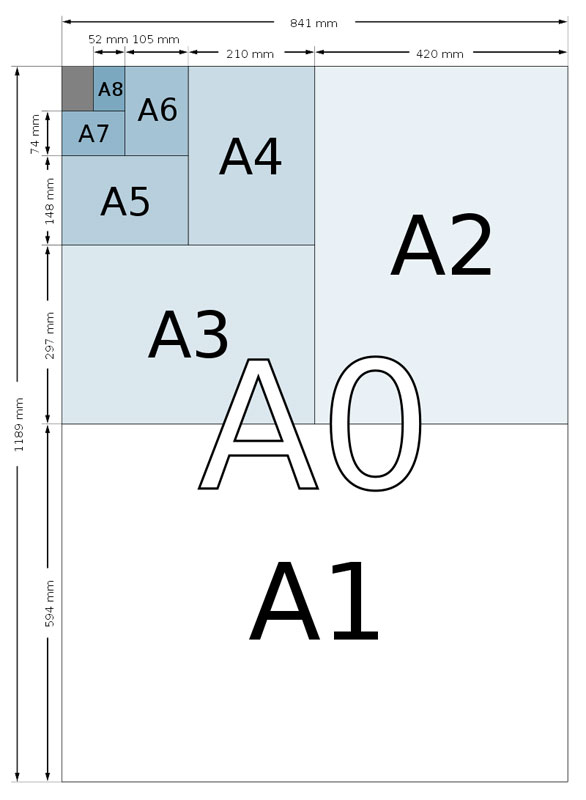
Από εκεί και πέρα, η διαδικασία είναι απλή: παίρνεις το Α0 και το κόβεις στη μέση (προσοχή, κόβεις πάντα από τη μεγαλύτερη πλευρά), παίρνοντας δύο φύλλα Α1. Κάνεις το ίδιο με το Α1 και παίρνεις το Α2. Κόβεις το Α2 και παίρνεις το Α3. Και, τέλος, κόβεις το Α3 για να φτάσεις στο αγαπημένο μας Α4.

Κάθε φορά που μειώνεις το μέγεθος, η αναλογία μήκος προς πλάτος παραμένει σταθερή και είναι √2:1.

Η Απόδειξη που Δένει το Γραφείο με τα Μαθηματικά

Ας δούμε τον λόγο των διαστάσεων για το αρχικό φύλλο χαρτιού Α0, το οποίο έχει διαστάσεις 1189mm×841mm:

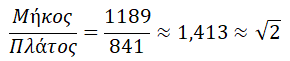
Αν τώρα ένα φύλλο χαρτιού έχει μήκος x και πλάτος y ώστε, x/y=√2 τότε αν το διπλώσουμε ο λόγος, μήκος y προς πλάτος x/2 , θα είναι:

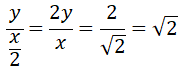
Άρα, ο λόγος των διαστάσεων παραμένει √2 οπότε διατηρείται η αναλογία σε κάθε διαδοχικό κόψιμο.

Αυτή η απλή μαθηματική συνθήκη είναι που καθιστά το σύστημα ISO 216 τόσο επαναστατικό…

Αυτό το σύστημα δεν είναι απλά μια μαθηματική σπαζοκεφαλιά, είναι μια πανέξυπνη λύση που έφερε επανάσταση στα γραφεία, εξοικονομώντας χρόνο και χρήμα. Το σημαντικότερο πλεονέκτημα είναι η Τέλεια Σμίκρυνση και Μεγέθυνση (Scaling). Όταν θες να φωτοτυπήσεις ένα κείμενο από Α4 σε Α3 (μεγέθυνση) ή από Α3 σε Α4 (σμίκρυνση) κλπ, το περιεχόμενο ταιριάζει τέλεια χωρίς να χρειάζεται να παραμορφωθεί ή να κοπούν τμήματα. Παράλληλα, η Τέλεια Δίπλωση σημαίνει ότι ένα διπλωμένο Α4 χωράει πάντα σωστά σε έναν φάκελο, απλοποιώντας την ταχυδρόμηση. Τέλος, υπάρχει η Οικονομία στην Παραγωγή: επειδή όλα τα μεγέθη είναι παράγωγα του 1m² του Α0, οι παραγωγοί μπορούν να κόψουν όλες τις άλλες διαστάσεις με μηδενική πρακτικά σπατάλη.

Την επόμενη φορά που θα κρατήσετε ένα φύλλο Α4, θυμηθείτε: δεν είναι απλώς ένα κομμάτι χαρτί. Είναι ένα μνημείο της πρακτικής ομορφιάς των Μαθηματικών. Το 29,7 εκατοστά δεν είναι τυχαία επιλογή. Είναι η απόδειξη ότι ακόμη και οι άρρητοι αριθμοί –αυτοί με τα άπειρα και ανεξέλεγκτα δεκαδικά ψηφία – μπορούν να αποτελέσουν τον θεμέλιο λίθο για ένα από τα πιο τυπικά και αναντικατάστατα εργαλεία της καθημερινότητάς μας.

Ο αριθμός √2 δεν είναι μόνο μια ρίζα ενός αριθμού, είναι η κρυφή αρχή της τάξης στον κόσμο του γραφείου μας. Και αυτό είναι... μ α γ ι κ ό !